Λειτουργία κατασκευής
Προσφέρουμε στην προσοχή σας μια υπηρεσία για την κατασκευή γραφημάτων συναρτήσεων στο Διαδίκτυο, των οποίων όλα τα δικαιώματα ανήκουν στην εταιρεία Δεσμός. Χρησιμοποιήστε την αριστερή στήλη για να εισαγάγετε συναρτήσεις. Μπορείτε να εισαγάγετε χειροκίνητα ή χρησιμοποιώντας το εικονικό πληκτρολόγιο στο κάτω μέρος του παραθύρου. Για να μεγεθύνετε το παράθυρο με το γράφημα, μπορείτε να αποκρύψετε τόσο την αριστερή στήλη όσο και το εικονικό πληκτρολόγιο.
Οφέλη από τη διαδικτυακή χαρτογράφηση
- Οπτική εμφάνιση των εισαγόμενων λειτουργιών
- Δημιουργία πολύ περίπλοκων γραφημάτων
- Κατασκευή γραφημάτων που καθορίζονται σιωπηρά (για παράδειγμα, έλλειψη x^2/9+y^2/16=1)
- Η δυνατότητα αποθήκευσης γραφημάτων και λήψης συνδέσμου προς αυτά, η οποία γίνεται διαθέσιμη σε όλους στο Διαδίκτυο
- Έλεγχος κλίμακας, χρώμα γραμμής
- Δυνατότητα σχεδίασης γραφημάτων ανά σημεία, με χρήση σταθερών
- Σχεδίαση πολλών γραφημάτων συναρτήσεων ταυτόχρονα
- Σχεδίαση σε πολικές συντεταγμένες (χρησιμοποιήστε r και θ(\theta))
Μαζί μας είναι εύκολο να δημιουργήσετε γραφήματα διαφορετικής πολυπλοκότητας στο διαδίκτυο. Η κατασκευή γίνεται άμεσα. Η υπηρεσία είναι περιζήτητη για την εύρεση σημείων τομής συναρτήσεων, για την απεικόνιση γραφημάτων για περαιτέρω μεταφορά τους σε ένα έγγραφο του Word ως εικονογραφήσεις κατά την επίλυση προβλημάτων και για την ανάλυση των χαρακτηριστικών συμπεριφοράς των γραφημάτων συναρτήσεων. Το βέλτιστο πρόγραμμα περιήγησης για εργασία με γραφήματα σε αυτήν τη σελίδα ιστότοπου είναι το Google Chrome. Η σωστή λειτουργία δεν είναι εγγυημένη όταν χρησιμοποιείτε άλλα προγράμματα περιήγησης.
Ας επιλέξουμε ένα ορθογώνιο σύστημα συντεταγμένων στο επίπεδο και ας σχεδιάσουμε τις τιμές του ορίσματος στον άξονα της τετμημένης Χ, και στην τεταγμένη - οι τιμές της συνάρτησης y = f(x).
Γράφημα συνάρτησης y = f(x)είναι το σύνολο όλων των σημείων των οποίων οι τετμημένες ανήκουν στο πεδίο ορισμού της συνάρτησης και οι τεταγμένες είναι ίσες με τις αντίστοιχες τιμές της συνάρτησης.
Με άλλα λόγια, η γραφική παράσταση της συνάρτησης y = f (x) είναι το σύνολο όλων των σημείων του επιπέδου, συντεταγμένες Χ, στοπου ικανοποιούν τη σχέση y = f(x).

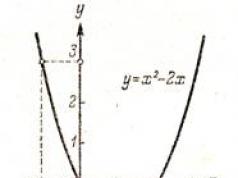
Στο Σχ. Τα 45 και 46 δείχνουν γραφήματα συναρτήσεων y = 2x + 1Και y = x 2 - 2x.
Αυστηρά μιλώντας, θα πρέπει να γίνει διάκριση μεταξύ ενός γραφήματος μιας συνάρτησης (ο ακριβής μαθηματικός ορισμός της οποίας δόθηκε παραπάνω) και μιας σχεδιασμένης καμπύλης, η οποία δίνει πάντα μόνο ένα περισσότερο ή λιγότερο ακριβές σκίτσο του γραφήματος (και ακόμη και τότε, κατά κανόνα, όχι ολόκληρο το γράφημα, αλλά μόνο το τμήμα του που βρίσκεται στα τελικά μέρη του επιπέδου). Σε αυτό που ακολουθεί, ωστόσο, θα λέμε γενικά "γραφική παράσταση" αντί "σκίτσο γραφήματος".
Χρησιμοποιώντας ένα γράφημα, μπορείτε να βρείτε την τιμή μιας συνάρτησης σε ένα σημείο. Δηλαδή, αν το σημείο x = αανήκει στο πεδίο ορισμού της συνάρτησης y = f(x), στη συνέχεια για να βρείτε τον αριθμό φά)(δηλαδή οι τιμές συνάρτησης στο σημείο x = α) θα πρέπει να το κάνετε αυτό. Είναι απαραίτητο μέσω του σημείου της τετμημένης x = ασχεδιάστε μια ευθεία γραμμή παράλληλη προς τον άξονα τεταγμένων. αυτή η γραμμή θα τέμνει το γράφημα της συνάρτησης y = f(x)σε ένα σημείο; η τεταγμένη αυτού του σημείου, δυνάμει του ορισμού του γραφήματος, θα είναι ίση με φά)(Εικ. 47).

Για παράδειγμα, για τη συνάρτηση f(x) = x 2 - 2xχρησιμοποιώντας το γράφημα (Εικ. 46) βρίσκουμε f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 κ.λπ.
Ένα γράφημα συνάρτησης απεικονίζει ξεκάθαρα τη συμπεριφορά και τις ιδιότητες μιας συνάρτησης. Για παράδειγμα, από την εξέταση του Σχ. 46 είναι σαφές ότι η συνάρτηση y = x 2 - 2xπαίρνει θετικές τιμές όταν Χ< 0 και στο x > 2, αρνητικό - στο 0< x < 2; наименьшее значение функция y = x 2 - 2xδέχεται στο x = 1.
Να γραφεί μια συνάρτηση f(x)πρέπει να βρείτε όλα τα σημεία του επιπέδου, συντεταγμένες Χ,στοπου ικανοποιούν την εξίσωση y = f(x). Στις περισσότερες περιπτώσεις, αυτό είναι αδύνατο να γίνει, αφού υπάρχει άπειρος αριθμός τέτοιων σημείων. Επομένως, το γράφημα της συνάρτησης απεικονίζεται κατά προσέγγιση - με μεγαλύτερη ή μικρότερη ακρίβεια. Η απλούστερη είναι η μέθοδος δημιουργίας γραφήματος χρησιμοποιώντας πολλά σημεία. Συνίσταται στο γεγονός ότι το επιχείρημα Χδώστε έναν πεπερασμένο αριθμό τιμών - ας πούμε, x 1, x 2, x 3,..., x k και δημιουργήστε έναν πίνακα που περιλαμβάνει τις επιλεγμένες τιμές συνάρτησης.
Ο πίνακας μοιάζει με αυτό:
Έχοντας συντάξει έναν τέτοιο πίνακα, μπορούμε να περιγράψουμε αρκετά σημεία στο γράφημα της συνάρτησης y = f(x). Στη συνέχεια, συνδέοντας αυτά τα σημεία με μια ομαλή γραμμή, παίρνουμε μια κατά προσέγγιση άποψη του γραφήματος της συνάρτησης y = f(x).
Πρέπει να σημειωθεί, ωστόσο, ότι η μέθοδος γραφικής παράστασης πολλαπλών σημείων είναι πολύ αναξιόπιστη. Στην πραγματικότητα, η συμπεριφορά του γραφήματος μεταξύ των προβλεπόμενων σημείων και η συμπεριφορά του έξω από το τμήμα μεταξύ των ακραίων σημείων που λαμβάνονται παραμένει άγνωστη.
Παράδειγμα 1. Να γραφεί μια συνάρτηση y = f(x)κάποιος συνέταξε έναν πίνακα με τιμές ορίσματος και συναρτήσεων:
Τα αντίστοιχα πέντε σημεία φαίνονται στο Σχ. 48.

Με βάση τη θέση αυτών των σημείων, κατέληξε στο συμπέρασμα ότι η γραφική παράσταση της συνάρτησης είναι μια ευθεία γραμμή (που φαίνεται στο Σχ. 48 με τη διακεκομμένη γραμμή). Μπορεί αυτό το συμπέρασμα να θεωρηθεί αξιόπιστο; Αν δεν υπάρχουν πρόσθετες σκέψεις που να υποστηρίζουν αυτό το συμπέρασμα, δύσκολα μπορεί να θεωρηθεί αξιόπιστο. αξιόπιστος.
Για να τεκμηριώσετε τη δήλωσή μας, εξετάστε τη συνάρτηση
![]() .
.
Οι υπολογισμοί δείχνουν ότι οι τιμές αυτής της συνάρτησης στα σημεία -2, -1, 0, 1, 2 περιγράφονται ακριβώς στον παραπάνω πίνακα. Ωστόσο, το γράφημα αυτής της συνάρτησης δεν είναι καθόλου ευθεία γραμμή (φαίνεται στο Σχ. 49). Ένα άλλο παράδειγμα θα ήταν η συνάρτηση y = x + l + sinπx;Οι έννοιές του περιγράφονται επίσης στον παραπάνω πίνακα.

Αυτά τα παραδείγματα δείχνουν ότι στην «καθαρή» της μορφή η μέθοδος δημιουργίας γραφήματος χρησιμοποιώντας πολλά σημεία είναι αναξιόπιστη. Επομένως, για να σχεδιάσουμε ένα γράφημα μιας δεδομένης συνάρτησης, συνήθως προχωράμε ως εξής. Αρχικά, μελετάμε τις ιδιότητες αυτής της συνάρτησης, με τη βοήθεια της οποίας μπορούμε να φτιάξουμε ένα σκίτσο του γραφήματος. Στη συνέχεια, υπολογίζοντας τις τιμές της συνάρτησης σε πολλά σημεία (η επιλογή των οποίων εξαρτάται από τις καθιερωμένες ιδιότητες της συνάρτησης), βρίσκονται τα αντίστοιχα σημεία του γραφήματος. Και τέλος, μια καμπύλη σχεδιάζεται μέσα από τα κατασκευασμένα σημεία χρησιμοποιώντας τις ιδιότητες αυτής της συνάρτησης.
Θα εξετάσουμε μερικές (τις απλούστερες και πιο συχνά χρησιμοποιούμενες) ιδιότητες των συναρτήσεων που χρησιμοποιούνται για την εύρεση ενός σκίτσου γραφήματος αργότερα, αλλά τώρα θα δούμε μερικές κοινώς χρησιμοποιούμενες μεθόδους για την κατασκευή γραφημάτων.
Γράφημα της συνάρτησης y = |f(x)|.
Συχνά είναι απαραίτητο να σχεδιάσετε μια συνάρτηση y = |f(x)|, όπου f(x) -δεδομένη λειτουργία. Ας σας υπενθυμίσουμε πώς γίνεται αυτό. Ορίζοντας την απόλυτη τιμή ενός αριθμού, μπορούμε να γράψουμε
![]()
Αυτό σημαίνει ότι το γράφημα της συνάρτησης y =|f(x)|μπορεί να ληφθεί από το γράφημα, συνάρτηση y = f(x)ως εξής: όλα τα σημεία της γραφικής παράστασης της συνάρτησης y = f(x), των οποίων οι τεταγμένες είναι μη αρνητικές, θα πρέπει να παραμείνουν αμετάβλητες. περαιτέρω, αντί για τα σημεία της γραφικής παράστασης της συνάρτησης y = f(x)έχοντας αρνητικές συντεταγμένες, θα πρέπει να κατασκευάσετε τα αντίστοιχα σημεία στη γραφική παράσταση της συνάρτησης y = -f(x)(δηλαδή μέρος του γραφήματος της συνάρτησης
y = f(x), που βρίσκεται κάτω από τον άξονα Χ,πρέπει να αντανακλάται συμμετρικά γύρω από τον άξονα Χ).

Παράδειγμα 2.Γράφημα τη συνάρτηση y = |x|.
Ας πάρουμε το γράφημα της συνάρτησης y = x(Εικ. 50, α) και μέρος αυτού του γραφήματος στο Χ< 0 (που βρίσκεται κάτω από τον άξονα Χ) ανακλάται συμμετρικά σε σχέση με τον άξονα Χ. Ως αποτέλεσμα, παίρνουμε ένα γράφημα της συνάρτησης y = |x|(Εικ. 50, β).
Παράδειγμα 3. Γράφημα τη συνάρτηση y = |x 2 - 2x|.

Αρχικά, ας σχεδιάσουμε τη συνάρτηση y = x 2 - 2x.Η γραφική παράσταση αυτής της συνάρτησης είναι μια παραβολή, οι κλάδοι της οποίας κατευθύνονται προς τα πάνω, η κορυφή της παραβολής έχει συντεταγμένες (1; -1), η γραφική παράσταση της τέμνει τον άξονα x στα σημεία 0 και 2. Στο διάστημα (0; 2) η συνάρτηση παίρνει αρνητικές τιμές, επομένως αυτό το τμήμα του γραφήματος ανακλάται συμμετρικά σε σχέση με τον άξονα της τετμημένης. Το σχήμα 51 δείχνει το γράφημα της συνάρτησης y = |x 2 -2x|, με βάση το γράφημα της συνάρτησης y = x 2 - 2x
Γράφημα της συνάρτησης y = f(x) + g(x)
Εξετάστε το πρόβλημα της κατασκευής γραφήματος μιας συνάρτησης y = f(x) + g(x).αν δίνονται γραφήματα συναρτήσεων y = f(x)Και y = g(x).
Σημειώστε ότι το πεδίο ορισμού της συνάρτησης y = |f(x) + g(x)| είναι το σύνολο όλων εκείνων των τιμών του x για τις οποίες ορίζονται και οι δύο συναρτήσεις y = f(x) και y = g(x), δηλαδή αυτό το πεδίο ορισμού είναι η τομή των τομέων ορισμού, συναρτήσεις f(x) και g(x).
Αφήστε τα σημεία (x 0 , y 1) Και (x 0, y 2) ανήκουν αντίστοιχα στις γραφικές παραστάσεις των συναρτήσεων y = f(x)Και y = g(x), δηλαδή y 1 = f (x 0), y 2 = g (x 0).Τότε το σημείο (x0;. y1 + y2) ανήκει στη γραφική παράσταση της συνάρτησης y = f(x) + g(x)(Για f(x 0) + g(x 0) = y 1 +y2),. και οποιοδήποτε σημείο στη γραφική παράσταση της συνάρτησης y = f(x) + g(x)μπορούν να ληφθούν με αυτόν τον τρόπο. Επομένως, το γράφημα της συνάρτησης y = f(x) + g(x)μπορεί να ληφθεί από γραφήματα συναρτήσεων y = f(x). Και y = g(x)αντικαθιστώντας κάθε σημείο ( x n, y 1) γραφικά λειτουργιών y = f(x)τελεία (x n, y 1 + y 2),Οπου y 2 = g(x n), δηλαδή μετατοπίζοντας κάθε σημείο ( x n, y 1) γράφημα συνάρτησης y = f(x)κατά μήκος του άξονα στοκατά το ποσό y 1 = g(x n). Στην περίπτωση αυτή λαμβάνονται υπόψη μόνο τέτοια σημεία Χ n για το οποίο ορίζονται και οι δύο συναρτήσεις y = f(x)Και y = g(x).
Αυτή η μέθοδος σχεδίασης μιας συνάρτησης y = f(x) + g(x) ονομάζεται πρόσθεση γραφημάτων συναρτήσεων y = f(x)Και y = g(x)
Παράδειγμα 4. Στο σχήμα κατασκευάστηκε ένα γράφημα της συνάρτησης με τη μέθοδο της προσθήκης γραφημάτων
y = x + sinx.
Όταν σχεδιάζετε μια συνάρτηση y = x + sinxτο σκεφτήκαμε f(x) = x,ΕΝΑ g(x) = sinx.Για να σχεδιάσουμε το γράφημα συνάρτησης, επιλέγουμε σημεία με τετμημένα -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Τιμές f(x) = x, g(x) = sinx, y = x + sinxΑς υπολογίσουμε στα επιλεγμένα σημεία και ας τοποθετήσουμε τα αποτελέσματα στον πίνακα.
Προηγουμένως, μελετήσαμε άλλες συναρτήσεις, για παράδειγμα γραμμικές, ας θυμηθούμε την τυπική της μορφή:
εξ ου και η προφανής θεμελιώδης διαφορά - στη γραμμική συνάρτηση Χβρίσκεται στον πρώτο βαθμό, και στη νέα λειτουργία που αρχίζουμε να μελετάμε, Χστέκεται στη δεύτερη δύναμη.
Θυμηθείτε ότι η γραφική παράσταση μιας γραμμικής συνάρτησης είναι μια ευθεία γραμμή και η γραφική παράσταση μιας συνάρτησης, όπως θα δούμε, είναι μια καμπύλη που ονομάζεται παραβολή.
Ας ξεκινήσουμε ανακαλύπτοντας από πού προήλθε ο τύπος. Η εξήγηση είναι η εξής: αν μας δοθεί ένα τετράγωνο με πλευρά ΕΝΑ, τότε μπορούμε να υπολογίσουμε το εμβαδόν του ως εξής:
Αν αλλάξουμε το μήκος της πλευράς ενός τετραγώνου, τότε το εμβαδόν του θα αλλάξει.
Έτσι, αυτός είναι ένας από τους λόγους για τους οποίους μελετάται η συνάρτηση
Θυμηθείτε ότι η μεταβλητή Χ- αυτή είναι μια ανεξάρτητη μεταβλητή ή όρισμα· σε μια φυσική ερμηνεία, μπορεί να είναι, για παράδειγμα, χρόνος. Η απόσταση είναι, αντίθετα, μια εξαρτημένη μεταβλητή· εξαρτάται από τον χρόνο. Η εξαρτημένη μεταβλητή ή συνάρτηση είναι μια μεταβλητή στο.
Αυτός είναι ο νόμος της αντιστοιχίας, σύμφωνα με τον οποίο κάθε τιμή Χεκχωρείται μία μόνο τιμή στο.
Οποιοσδήποτε νόμος αντιστοιχίας πρέπει να ικανοποιεί την απαίτηση της μοναδικότητας από όρισμα σε λειτουργία. Σε μια φυσική ερμηνεία, αυτό φαίνεται αρκετά ξεκάθαρο χρησιμοποιώντας το παράδειγμα της εξάρτησης της απόστασης από τον χρόνο: σε κάθε χρονική στιγμή βρισκόμαστε σε μια ορισμένη απόσταση από το σημείο εκκίνησης και είναι αδύνατο να είμαστε τόσο 10 όσο και 20 χιλιόμετρα από την αρχή του ταξιδιού την ίδια στιγμή την ώρα t.
Ταυτόχρονα, κάθε τιμή συνάρτησης μπορεί να επιτευχθεί με πολλές τιμές ορίσματος.
Άρα, πρέπει να φτιάξουμε ένα γράφημα της συνάρτησης, για αυτό πρέπει να φτιάξουμε έναν πίνακα. Στη συνέχεια μελετήστε τη συνάρτηση και τις ιδιότητές της χρησιμοποιώντας το γράφημα. Αλλά ακόμη και πριν κατασκευάσουμε ένα γράφημα με βάση τον τύπο της συνάρτησης, μπορούμε να πούμε κάτι για τις ιδιότητές της: είναι προφανές ότι στοδεν μπορεί να λάβει αρνητικές τιμές, αφού
Λοιπόν, ας κάνουμε έναν πίνακα:

Ρύζι. 1
Από το γράφημα είναι εύκολο να σημειωθούν οι ακόλουθες ιδιότητες:
Αξονας στο- αυτός είναι ο άξονας συμμετρίας του γραφήματος.
Η κορυφή της παραβολής είναι το σημείο (0; 0).
Βλέπουμε ότι η συνάρτηση δέχεται μόνο μη αρνητικές τιμές.
Στο διάστημα όπου ![]() η συνάρτηση μειώνεται και στο διάστημα όπου αυξάνεται η συνάρτηση.
η συνάρτηση μειώνεται και στο διάστημα όπου αυξάνεται η συνάρτηση.
Η συνάρτηση αποκτά τη μικρότερη τιμή της στην κορυφή, ![]() ;
;
Δεν υπάρχει η μεγαλύτερη τιμή μιας συνάρτησης.
Παράδειγμα 1
Κατάσταση:
![]()
Λύση:
Επειδή η Χανά συνθήκη αλλάζει σε ένα συγκεκριμένο διάστημα, μπορούμε να πούμε για τη συνάρτηση ότι αυξάνεται και αλλάζει στο διάστημα . Η συνάρτηση έχει μια ελάχιστη τιμή και μια μέγιστη τιμή σε αυτό το διάστημα

Ρύζι. 2. Γράφημα της συνάρτησης y = x 2 , x ∈
Παράδειγμα 2
Κατάσταση:Βρείτε τη μεγαλύτερη και τη μικρότερη τιμή μιας συνάρτησης:
![]()
Λύση:
Χαλλάζει στο μεσοδιάστημα, που σημαίνει στομειώνεται στο διάστημα ενώ και αυξάνεται στο διάστημα ενώ .
Άρα, τα όρια της αλλαγής Χ, και τα όρια της αλλαγής στο, και, επομένως, σε ένα δεδομένο διάστημα υπάρχει και μια ελάχιστη τιμή της συνάρτησης και μια μέγιστη

Ρύζι. 3. Γράφημα της συνάρτησης y = x 2 , x ∈ [-3; 2]
Ας δείξουμε το γεγονός ότι η ίδια τιμή συνάρτησης μπορεί να επιτευχθεί με πολλές τιμές ορίσματος.
Μάθημα: Πώς να κατασκευάσετε μια παραβολή ή μια τετραγωνική συνάρτηση;
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ
Η παραβολή είναι μια γραφική παράσταση μιας συνάρτησης που περιγράφεται με τον τύπο ax 2 +bx+c=0.
Για να φτιάξετε μια παραβολή πρέπει να ακολουθήσετε έναν απλό αλγόριθμο:
1) Τύπος παραβολής y=ax 2 +bx+c,
Αν a>0τότε κατευθύνονται οι κλάδοι της παραβολής πάνω,
διαφορετικά οι κλάδοι της παραβολής κατευθύνονται κάτω.
Δωρεάν μέλος ντοΑυτό το σημείο τέμνει την παραβολή με τον άξονα OY.
2), βρίσκεται χρησιμοποιώντας τον τύπο x=(-b)/2a, αντικαθιστούμε το ευρεθέν x στην εξίσωση της παραβολής και βρίσκουμε y;
3)Συναρτήσεις μηδενικάή, με άλλα λόγια, τα σημεία τομής της παραβολής με τον άξονα ΟΧ, ονομάζονται και ρίζες της εξίσωσης. Για να βρούμε τις ρίζες εξισώνουμε την εξίσωση με 0 ax 2 +bx+c=0;
Τύποι εξισώσεων:
α) Η πλήρης τετραγωνική εξίσωση έχει τη μορφή ax 2 +bx+c=0και λύνεται από το διακριτικό?
β) Ημιτελής δευτεροβάθμια εξίσωση της φόρμας τσεκούρι 2 +bx=0.Για να το λύσετε, πρέπει να βγάλετε το x από αγκύλες και, στη συνέχεια, να εξισώσετε κάθε παράγοντα με 0:
τσεκούρι 2 +bx=0,
x(ax+b)=0,
x=0 και ax+b=0;
γ) Ημιτελής δευτεροβάθμια εξίσωση της φόρμας τσεκούρι 2 +γ=0.Για να το λύσετε, πρέπει να μετακινήσετε τα άγνωστα στη μία πλευρά και τα γνωστά στην άλλη. x =±√(c/a);
4) Βρείτε πολλά επιπλέον σημεία για να κατασκευάσετε τη συνάρτηση.
ΠΡΑΚΤΙΚΟ ΜΕΡΟΣ
Και έτσι τώρα, χρησιμοποιώντας ένα παράδειγμα, θα αναλύσουμε τα πάντα βήμα προς βήμα:
Παράδειγμα #1:
y=x 2 +4x+3
c=3 σημαίνει ότι η παραβολή τέμνει το OY στο σημείο x=0 y=3. Οι κλάδοι της παραβολής κοιτούν ψηλά αφού a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 κορυφή βρίσκεται στο σημείο (-2;-1)
Ας βρούμε τις ρίζες της εξίσωσης x 2 +4x+3=0
Χρησιμοποιώντας το διακριτικό βρίσκουμε τις ρίζες
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Ας πάρουμε πολλά αυθαίρετα σημεία που βρίσκονται κοντά στην κορυφή x = -2
x -4 -3 -1 0
y 3 0 0 3
Αντικαταστήστε αντί του x στην εξίσωση y=x 2 +4x+3 τιμές
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Από τις τιμές της συνάρτησης φαίνεται ότι η παραβολή είναι συμμετρική ως προς την ευθεία x = -2
Παράδειγμα #2:
y=-x 2 +4x
c=0 σημαίνει ότι η παραβολή τέμνει το OY στο σημείο x=0 y=0. Οι κλάδοι της παραβολής κοιτούν προς τα κάτω αφού a=-1 -1 Ας βρούμε τις ρίζες της εξίσωσης -x 2 +4x=0
Ημιτελής τετραγωνική εξίσωση της μορφής ax 2 +bx=0. Για να το λύσετε, πρέπει να βγάλετε το x από αγκύλες και μετά να εξισώσετε κάθε παράγοντα με 0.
x(-x+4)=0, x=0 και x=4.
Ας πάρουμε πολλά αυθαίρετα σημεία που βρίσκονται κοντά στην κορυφή x=2
x 0 1 3 4
y 0 3 3 0
Αντικαταστήστε αντί του x στην εξίσωση y=-x 2 +4x τιμές
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Από τις τιμές της συνάρτησης φαίνεται ότι η παραβολή είναι συμμετρική ως προς την ευθεία x = 2
Παράδειγμα Νο. 3
y=x 2 -4
c=4 σημαίνει ότι η παραβολή τέμνει το OY στο σημείο x=0 y=4. Οι κλάδοι της παραβολής κοιτούν ψηλά αφού a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 η κορυφή βρίσκεται στο σημείο (0;- 4 )
Ας βρούμε τις ρίζες της εξίσωσης x 2 -4=0
Ημιτελής τετραγωνική εξίσωση της μορφής ax 2 +c=0. Για να το λύσετε, πρέπει να μετακινήσετε τα άγνωστα στη μία πλευρά και τα γνωστά στην άλλη. x =±√(c/a)
x 2 =4
x 1 =2
x 2 =-2
Ας πάρουμε πολλά αυθαίρετα σημεία που βρίσκονται κοντά στην κορυφή x=0
x -2 -1 1 2
y 0 -3 -3 0
Αντικαταστήστε αντί του x στην εξίσωση y= x 2 -4 τιμές
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Μπορεί να φανεί από τις τιμές της συνάρτησης ότι η παραβολή είναι συμμετρική ως προς την ευθεία x = 0
Εγγραφείτε στο κανάλι στο YOUTUBEγια να ενημερώνεστε για όλα τα νέα προϊόντα και να προετοιμαστείτε μαζί μας για εξετάσεις.
"Φυσικός λογάριθμος" - 0,1. Φυσικοί λογάριθμοι. 4. Λογαριθμικά βελάκια. 0,04. 7.121.
“Power function grade 9” - U. Κυβική παραβολή. Υ = x3. Δάσκαλος 9ης τάξης Ladoshkina I.A. Υ = x2. Υπερβολή. 0. Y = xn, y = x-n όπου n είναι ένας δεδομένος φυσικός αριθμός. Χ. Ο εκθέτης είναι άρτιος φυσικός αριθμός (2n).
«Τετραγωνική συνάρτηση» - 1 Ορισμός τετραγωνικής συνάρτησης 2 Ιδιότητες συνάρτησης 3 Γραφήματα μιας συνάρτησης 4 Τετραγωνικές ανισώσεις 5 Συμπέρασμα. Ιδιότητες: Ανισότητες: Προετοιμάστηκε από τον μαθητή της 8Α τάξης Andrey Gerlitz. Σχέδιο: Γράφημα: -Διαστήματα μονοτονίας για α > 0 για α< 0. Квадратичная функция. Квадратичные функции используются уже много лет.
«Η τετραγωνική συνάρτηση και η γραφική της παράσταση» - Λύση.y=4x A(0.5:1) 1=1 A-ανήκει. Όταν a=1, ο τύπος y=ax παίρνει τη μορφή.
«Τετραγωνική συνάρτηση 8ης τάξης» - 1) Κατασκευάστε την κορυφή μιας παραβολής. Σχεδιάζοντας μια γραφική παράσταση μιας τετραγωνικής συνάρτησης. Χ. -7. Κατασκευάστε ένα γράφημα της συνάρτησης. Άλγεβρα 8η τάξη Δάσκαλος 496 Bovina school T.V. -1. Σχέδιο κατασκευής. 2) Κατασκευάστε τον άξονα συμμετρίας x=-1. y.