Побудувати функцію
Ми пропонуємо до вашої уваги сервіс з потроєння графіків функцій онлайн, всі права на який належать компанії Desmos. Для введення функцій скористайтесь лівою колонкою. Можна вводити вручну або за допомогою віртуальної клавіатури внизу вікна. Для збільшення вікна з графіком можна приховати як ліву колонку, і віртуальну клавіатуру.
Переваги побудови графіків онлайн
- Візуальне відображення функцій, що вводяться
- Побудова дуже складних графіків
- Побудова графіків, заданих неявно (наприклад, еліпс x^2/9+y^2/16=1)
- Можливість зберігати графіки та отримувати на них посилання, яке стає доступним для всіх в інтернеті.
- Управління масштабом, кольором ліній
- Можливість побудови графіків за точками, використання констант
- Побудова одночасно кількох графіків функцій
- Побудова графіків у полярній системі координат (використовуйте r та θ(\theta))
З нами легко в режимі онлайн будувати графіки різної складності. Побудова провадиться миттєво. Сервіс затребуваний знаходження точок перетину функцій, зображення графіків для подальшого їх переміщення у Word документ як ілюстрацій під час вирішення завдань, для аналізу поведінкових особливостей графіків функций. Оптимальним браузером для роботи з графіками на цій сторінці є Google Chrome. У разі використання інших браузерів коректність роботи не гарантується.
Виберемо на площині прямокутну систему координат і відкладатимемо на осі абсцис значення аргументу х, але в осі ординат - значення функції у = f(х).
Графіком функції y = f(x)називається безліч всіх точок, у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.
Іншими словами, графік функції y = f(х) - це безліч усіх точок площини, координати х, уяких задовольняють співвідношення y = f(x).

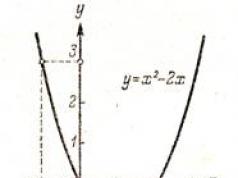
На рис. 45 та 46 наведено графіки функцій у = 2х + 1і у = х 2 - 2х.
Строго кажучи, слід розрізняти графік функції (точне математичне визначення якого було дано вище) і накреслену криву, яка завжди дає лише більш менш точний ескіз графіка (та й те, як правило, не всього графіка, а лише його частини, розташованого в кінцевій частини площини). Надалі, однак, ми зазвичай говоритимемо «графік», а не «ескіз графіка».
За допомогою графіка можна знаходити значення функції у точці. Саме, якщо точка х = аналежить області визначення функції y = f(x), то для знаходження числа f(а)(тобто значення функції у точці х = а) слід вчинити так. Потрібно через крапку з абсцисою х = апровести пряму, паралельну осі ординат; ця пряма перетне графік функції y = f(x)в одній точці; ордината цієї точки і буде, з визначення графіка, дорівнює f(а)(Рис. 47).

Наприклад, для функції f(х) = х 2 - 2xза допомогою графіка (рис. 46) знаходимо f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 і т.д.
Графік функції наочно ілюструє поведінку та властивості функції. Наприклад, із розгляду рис. 46 ясно, що функція у = х 2 - 2хнабуває позитивних значень при х< 0 і при х > 2, Негативні - при 0< x < 2; наименьшее значение функция у = х 2 - 2хприймає за х = 1.
Для побудови графіка функції f(x)потрібно знайти всі точки площини, координати х,уяких задовольняють рівняння y = f(x). Найчастіше це зробити неможливо, оскільки таких точок нескінченно багато. Тому графік функції зображують приблизно з більшою або меншою точністю. Найпростішим є метод побудови графіка за кількома точками. Він у тому, що аргументу хнадають кінцеве число значень - скажімо, х 1, х 2, x 3, ..., х k і становлять таблицю, до якої входять вибрані значення функції.
Таблиця виглядає так:
Склавши таку таблицю, ми можемо намітити кілька точок графіка функції y = f(x). Потім, з'єднуючи ці точки плавною лінією, ми отримуємо приблизний вид графіка функції y = f(x).
Слід зазначити, що метод побудови графіка за кількома точками дуже ненадійний. Насправді поведінка графіка між наміченими точками та поведінка його поза відрізком між крайніми зі взятих точок залишається невідомою.
Приклад 1. Для побудови графіка функції y = f(x)хтось склав таблицю значень аргументу та функції:
Відповідні п'ять точок показано на рис. 48.

На підставі розташування цих точок він зробив висновок, що графік функції є прямою (показану на рис. 48 пунктиром). Чи можна вважати цей висновок надійним? Якщо немає додаткових міркувань, які б підтверджували цей висновок, його навряд чи можна вважати надійним. надійним.
Для обґрунтування свого твердження розглянемо функцію
![]() .
.
Обчислення показують, що значення цієї функції в точках -2, -1, 0, 1, 2 описуються наведеною вище таблицею. Однак графік цієї функції не є прямою лінією (він показаний на рис. 49). Іншим прикладом може бути функція y = x + l + sinπx;її значення теж описуються наведеною вище таблицею.

Ці приклади показують, що у «чистому» вигляді метод побудови графіка за кількома точками ненадійний. Тому для побудови графіка заданої функції, як правило, надходять у такий спосіб. Спочатку вивчають властивості цієї функції, з допомогою яких можна побудувати ескіз графіка. Потім, обчислюючи значення функції кількох точках (вибір яких залежить від встановлених властивостей функції), знаходять відповідні точки графіка. І, нарешті, через побудовані точки проводять криву, використовуючи властивості цієї функції.
Деякі (найпростіші і найчастіше використовувані) властивості функцій, застосовувані перебування ескізу графіка, ми розглянемо пізніше, тепер розберемо деякі часто застосовувані методи побудови графіків.
Графік функції у = | f (x) |.
Нерідко доводиться будувати графік функції y = | f (x)|, де f(х) -задана функція. Нагадаємо, як це робиться. За визначенням абсолютної величини числа можна написати
![]()
Це означає, що графік функції y = | f (x) |можна отримати з графіка, функції y = f(x)наступним чином: всі точки графіка функції у = f(х), у яких ординати невід'ємні, слід залишити без зміни; далі, замість точок графіка функції y = f(x), що мають негативні координати, слід побудувати відповідні точки графіка функції у = -f(x)(тобто частина графіка функції
y = f(x), що лежить нижче осі х,слід симетрично відобразити щодо осі х).

приклад 2.Побудувати графік функції у = | х |.
Беремо графік функції у = х(рис. 50, а) та частина цього графіка при х< 0 (що лежить під віссю х) симетрично відбиваємо щодо осі х. В результаті ми отримуємо графік функції у = | х |(Рис. 50, б).
Приклад 3. Побудувати графік функції y = | x 2 - 2x |.

Спочатку збудуємо графік функції y = x 2 – 2x.Графік цієї функції - парабола, гілки якої спрямовані вгору, вершина параболи має координати (1; -1), її графік перетинає вісь абсцис у точках 0 і 2. На проміжку (0; 2) фукція набуває негативних значень, тому саме цю частину графіка симетрично відобразимо щодо осі абсцис. На малюнку 51 побудовано графік функції у = | х 2 -2х |виходячи з графіка функції у = х 2 - 2x
Графік функції y = f(x) + g(x)
Розглянемо задачу побудови графіка функції y = f(x) + g(x).якщо задані графіки функцій y = f(x)і y = g(x).
Зауважимо, що область визначення функції y = |f(x) + g(х)| є безліч всіх тих значень х, для яких визначені обидві функції y = f(x) і у = g(х), тобто ця область визначення є перетином областей визначення, функцій f(x) і g(x).
Нехай крапки (х 0 , y 1) та (х 0, у 2) відповідно належать графікам функцій y = f(x)і y = g(х), Т. е. y 1 = f(x0), y2=g(х0).Тоді точка (x0;. y1 + y2) належить графіку функції у = f(х) + g(х)(бо f(х 0) + g(x 0) = y 1+y2),. причому будь-яка точка графіка функції y = f(x) + g(x)може бути отримана в такий спосіб. Отже, графік функції у = f(x) + g(x)можна отримати з графіків функцій y = f(x). і y = g(х)заміною кожної точки ( х n , у 1) графік функції y = f(x)точкою (х n, y 1 + y 2),де у 2 = g(x n), тобто зсувом кожної точки ( х n , у 1) графіка функції y = f(x)вздовж осі уна величину y 1 = g(х n). При цьому розглядаються лише такі точки х n для яких визначено обидві функції y = f(x)і y = g(x).
Такий метод побудови графіка функції y = f(x) + g(х) називається додаванням графіків функцій y = f(x)і y = g(x)
Приклад 4. На малюнку методом складання графіків побудовано графік функції
y = x + sinx.
При побудові графіка функції y = x + sinxми вважали, що f(x) = x,а g(x) = sinx.Для побудови графіка функції виберемо крапки з aбцисами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значення f(x) = x, g(x) = sinx, y = x + sinxобчислимо у вибраних точках і результати помістимо у таблиці.
Раніше ми вивчали інші функції, наприклад лінійну, нагадаємо її стандартний вигляд:
звідси очевидна принципова відмінність - у лінійній функції хстоїть у першому ступені, а в тій новій функції, до вивчення якої ми приступаємо, хстоїть у другому ступені.
Нагадаємо, що графіком лінійної функції є пряма лінія, а графіком функції, як ми побачимо, є крива, яка називається параболою.
Почнемо з того, що з'ясуємо, звідки з'явилася формула . Пояснення таке: якщо нам заданий квадрат зі стороною а, то площу його ми можемо обчислити так:
Якщо ми змінюватимемо довжину сторони квадрата, то і його площа змінюватиметься.
Отже, наведено одну з причин, через яку вивчається функція
Нагадаємо, що змінна х- це незалежна змінна, або аргумент, у фізичній інтерпретації це може бути, наприклад, час. Відстань це навпаки залежна змінна, вона залежить від часу. Залежною змінною або функцією називається змінна у.
Це закон відповідності, за яким кожному значенню хставиться у відповідність єдине значення у.
Будь-який закон відповідності має задовольняти вимогу єдиності від аргументу до функції. У фізичній інтерпретації це виглядає досить зрозуміло на прикладі залежності відстані від часу: у кожний момент часу ми знаходимося на якійсь конкретній відстані від початкового пункту, і неможливо одночасно в момент часу t знаходиться і за 10 і 20 кілометрів від початку шляху.
У той самий час кожне значення функції може досягатися за кількох значеннях аргументу.
Отже, потрібно побудувати графік функції , при цьому скласти таблицю. Потім за графіком досліджувати функцію та її властивості. Але вже до побудови графіка на вигляд функції ми можемо дещо сказати про її властивості: очевидно, що уне може набувати негативних значень, оскільки
Отже, складемо таблицю:

Мал. 1
За графіком неважко відзначити такі характеристики:
Ось у- це вісь симетрії графіка;
Вершина параболи – точка (0; 0);
Ми бачимо, що функція набуває лише невід'ємних значень;
На проміжку, де ![]() функція зменшується, але в проміжку, де функція зростає;
функція зменшується, але в проміжку, де функція зростає;
Найменше значення функція набуває у вершині, ![]() ;
;
Найбільшого значення функції немає;
Приклад 1
Умова:
![]()
Рішення:
Оскільки хза умовою змінюється на конкретному проміжку, можемо сказати про функції, що вона зростає та змінюється на проміжку . Функція має на цьому проміжку мінімальне значення та максимальне значення

Мал. 2. Графік функції y = x 2 x ∈
Приклад 2
Умова:Знайти найбільше та найменше значення функції:
![]()
Рішення:
хзмінюється на проміжку, значить узменшується на проміжку поки що і зростає на проміжку поки що.
Отже, межі зміни х, а межі зміни уа, отже, на даному проміжку існує і мінімальне значення функції , і максимальне

Мал. 3. Графік функції y = x 2 x ∈ [-3; 2]
Проілюструємо той факт, що те саме значення функції може досягатися при кількох значеннях аргументу.
Урок: як побудувати параболу чи квадратичну функцію?
ТЕОРЕТИЧНА ЧАСТИНА
Парабола — це графік функції, описаний формулою ax 2 +bx+c=0.
Щоб побудувати параболу потрібно слідувати простому алгоритму дій:
1) Формула параболи y=ax 2 +bx+c,
якщо а>0то гілки параболи направлені вгору,
а то гілки параболи спрямовані вниз.
Вільний член cця точка перетинається параболи з віссю OY;
2) , її знаходять за формулою x=(-b)/2aзнайдений x підставляємо в рівняння параболи і знаходимо y;
3)Нулі функціїабо інакше точки перетину параболи з віссю OX вони ще називаються корінням рівняння. Щоб знайти коріння ми рівняння прирівнюємо до 0 ax 2 +bx+c=0;
Види рівнянь:
a) Повне квадратне рівняння має вигляд ax 2 +bx+c=0і вирішується за дискримінантом;
b) Неповне квадратне рівняння виду ax 2 + bx = 0.Щоб його вирішити, потрібно винести х за дужки, потім кожен множник прирівняти до 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 та ax+b=0;
c)Неповне квадратне рівняння виду ax 2 + c = 0.Щоб його вирішити, потрібно невідомі перенести в один бік, а відомі в інший. x =±√(c/a);
4) Знайти кілька додаткових точок для побудови функції.
ПРАКТИЧНА ЧАСТИНА
І так тепер на прикладі розберемо все за діями:
Приклад №1:
y=x 2 +4x+3
c=3 означає парабола перетинає OY у точці х=0 у=3. Гілки параболи дивляться нагору оскільки а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 вершина знаходиться у точці (-2;-1)
Знайдемо коріння рівняння x2+4x+3=0
За дискримінантом знаходимо коріння
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Візьмемо кілька довільних точок, що знаходяться поруч із вершиною х=-2
х -4 -3 -1 0
у 3 0 0 3
Підставляємо замість х рівняння y=x 2 +4x+3 значення
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно за значеннями функції, що парабола симетрична щодо прямої х = -2
Приклад №2:
y=-x 2 +4x
c=0 означає парабола перетинає OY у точці х=0 у=0. Гілки параболи дивляться вниз оскільки а=-1 -1 Знайдемо коріння рівняння -x 2 +4x=0
Неповне квадратне рівняння виду ax2+bx=0. Щоб його вирішити, потрібно винести х за дужки, потім кожен множник прирівняти до 0.
х(-x+4)=0, х=0 та x=4.
Візьмемо кілька довільних точок, що знаходяться поруч із вершиною х=2
х 0 1 3 4
у 0 3 3 0
Підставляємо замість х рівняння y=-x 2 +4x значення
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно за значеннями функції, що парабола симетрична щодо прямої х = 2
Приклад №3
y=x 2 -4
c=4 означає парабола перетинає OY у точці х=0 у=4. Гілки параболи дивляться нагору оскільки а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина знаходиться в точці (0;-4 )
Знайдемо коріння рівняння x 2 -4 = 0
Неповне квадратне рівняння виду ax2+c=0. Щоб його вирішити, потрібно невідомі перенести в один бік, а відомі в інший. x =±√(c/a)
x 2 = 4
x 1 =2
x 2 =-2
Візьмемо кілька довільних точок, що знаходяться поруч із вершиною х=0
х -2 -1 1 2
у 0 -3 -3 0
Підставляємо замість х рівняння y= x 2 -4 значення
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно за значеннями функції, що парабола симетрична щодо прямої х = 0
Підписуйтесь на канал на YOUTUBEщоб бути в курсі всіх новинок і готується з нами до іспитів.
"Натуральний логарифм" - 0,1. Натуральні логарифми. 4. "Логарифмічний дартс". 0,04. 7. 121.
«Ступінна функція 9 клас» - У. Кубічна парабола. У = х3. 9 клас вчитель Ладошкіна І.А. У = х2. Гіперболу. 0. У = хn, у = х-n де n - задане натуральне число. Х. Показник – парне натуральне число (2n).
"Квадратична функція" - 1 Визначення квадратичної функції 2 Властивості функції 3 Графіки функції 4 Квадратичні нерівності 5 Висновок. Властивості: Нерівності: Підготував учень 8А класу Герліц Андрій. План: Графік: -проміжки монотонності при а > 0 при а< 0. Квадратичная функция. Квадратичные функции используются уже много лет.
«Квадратична функція та її графік» - Решение.у=4x А(0,5:1) 1=1 А-належить. При а=1 формула у=аx набуває вигляду.
«8 клас квадратична функція» - 1) Побудувати вершину параболи. Побудова графіка квадратичної функції. x. -7. Побудувати графік функції. Алгебра 8 клас Учитель 496 школи Бовіна Т. В. -1. План побудови. 2) Побудувати вісь симетрії x=-1. y.