Oluşturma işlevi
Tüm hakları şirkete ait olan, çevrimiçi fonksiyon grafikleri oluşturmaya yönelik bir hizmeti dikkatinize sunuyoruz. Desmos. İşlevlere girmek için sol sütunu kullanın. Manuel olarak veya pencerenin altındaki sanal klavyeyi kullanarak girebilirsiniz. Grafiğin bulunduğu pencereyi büyütmek için hem sol sütunu hem de sanal klavyeyi gizleyebilirsiniz.
Çevrimiçi grafiğin faydaları
- Girilen fonksiyonların görsel gösterimi
- Çok karmaşık grafikler oluşturma
- Örtülü olarak belirtilen grafiklerin oluşturulması (örneğin, elips x^2/9+y^2/16=1)
- İnternetteki herkesin kullanımına sunulan grafikleri kaydetme ve bunlara bir bağlantı alma yeteneği
- Ölçek kontrolü, çizgi rengi
- Sabitleri kullanarak grafikleri noktalara göre çizme imkanı
- Aynı anda birden fazla fonksiyon grafiğinin çizilmesi
- Kutupsal koordinatlarda çizim (r ve θ(\theta)) kullanın
Bizimle, çevrimiçi olarak değişen karmaşıklıktaki çizelgeleri oluşturmak kolaydır. İnşaat anında yapılır. Bu hizmet, fonksiyonların kesişim noktalarını bulmak, problemleri çözerken bunları bir Word belgesine taşımak için grafikleri tasvir etmek ve fonksiyon grafiklerinin davranışsal özelliklerini analiz etmek için talep görmektedir. Bu web sitesi sayfasındaki grafiklerle çalışmak için en uygun tarayıcı Google Chrome'dur. Diğer tarayıcılar kullanıldığında doğru çalışma garanti edilmez.
Düzlemde dikdörtgen bir koordinat sistemi seçelim ve argümanın değerlerini apsis eksenine çizelim. X ve ordinatta - fonksiyonun değerleri y = f(x).
Fonksiyon grafiği y = f(x) apsisleri fonksiyonun tanım alanına ait olan ve koordinatları fonksiyonun karşılık gelen değerlerine eşit olan tüm noktaların kümesidir.
Başka bir deyişle, y = f(x) fonksiyonunun grafiği düzlemin tüm noktalarının, koordinatlarının kümesidir X, en ilişkiyi tatmin eden y = f(x).

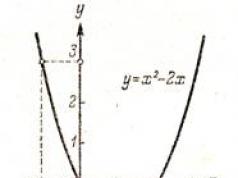
İncirde. 45 ve 46 fonksiyonların grafiklerini gösterir y = 2x + 1 Ve y = x 2 - 2x.
Kesin olarak konuşursak, bir fonksiyonun grafiği (tam matematiksel tanımı yukarıda verilmiştir) ile her zaman grafiğin az çok doğru bir taslağını veren (ve o zaman bile kural olarak) çizilmiş bir eğri arasında ayrım yapılmalıdır. grafiğin tamamı değil, yalnızca düzlemin son kısımlarında bulunan kısmı). Ancak bundan sonra genel olarak "grafik taslağı" yerine "grafik" diyeceğiz.
Bir grafiği kullanarak bir fonksiyonun değerini bir noktada bulabilirsiniz. Yani eğer nokta x = bir fonksiyonun tanım alanına aittir y = f(x), ardından numarayı bulmak için f(a)(yani noktadaki fonksiyon değerleri x = bir) Bunu yapmalısın. Apsis noktasından geçmek gerekiyor x = bir ordinat eksenine paralel düz bir çizgi çizin; bu çizgi fonksiyonun grafiğiyle kesişecek y = f(x) bir noktada; Grafiğin tanımı gereği bu noktanın ordinatı şuna eşit olacaktır: f(a)(Şek. 47).

Örneğin, fonksiyon için f(x) = x 2 - 2x Grafiği kullanarak (Şekil 46) f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 vb. buluruz.
Bir fonksiyon grafiği, bir fonksiyonun davranışını ve özelliklerini açıkça gösterir. Örneğin, Şekil 2'nin değerlendirilmesinden. 46, fonksiyonun açık olduğu açıktır. y = x 2 - 2x pozitif değerler aldığında X< 0 ve x > 2, negatif - 0'da< x < 2; наименьшее значение функция y = x 2 - 2x kabul eder x = 1.
Bir fonksiyonun grafiğini çizmek için f(x) uçağın tüm noktalarını, koordinatlarını bulmanız gerekiyor X,en denklemi sağlayan y = f(x). Çoğu durumda, bu tür noktaların sonsuz sayıda olması nedeniyle bunu yapmak imkansızdır. Bu nedenle, fonksiyonun grafiği yaklaşık olarak - daha fazla veya daha az doğrulukla - gösterilir. En basiti, birkaç noktayı kullanarak bir grafik çizme yöntemidir. Bu, argümanın şu gerçeğinden oluşur: X sonlu sayıda değer verin - örneğin x 1, x 2, x 3,..., x k ve seçilen fonksiyon değerlerini içeren bir tablo oluşturun.
Tablo şuna benziyor:
Böyle bir tabloyu derledikten sonra fonksiyonun grafiğinde birkaç noktayı özetleyebiliriz. y = f(x). Daha sonra bu noktaları düzgün bir çizgiyle birleştirerek fonksiyonun grafiğinin yaklaşık bir görünümünü elde ederiz. y = f(x).
Ancak çok noktalı çizim yönteminin çok güvenilmez olduğu unutulmamalıdır. Aslında grafiğin amaçlanan noktalar arasındaki davranışı ve alınan uç noktalar arasındaki segment dışındaki davranışı bilinmemektedir.
örnek 1. Bir fonksiyonun grafiğini çizmek için y = f(x) birisi argüman ve fonksiyon değerlerinden oluşan bir tablo derledi:
Karşılık gelen beş nokta Şekil 2'de gösterilmektedir. 48.

Bu noktaların konumuna dayanarak fonksiyonun grafiğinin düz bir çizgi olduğu sonucuna vardı (Şekil 48'de noktalı çizgiyle gösterilmiştir). Bu sonuç güvenilir sayılabilir mi? Bu sonucu destekleyecek ek hususlar olmadığı sürece, bunun güvenilir olduğu düşünülemez. güvenilir.
İfademizi doğrulamak için işlevi göz önünde bulundurun
![]() .
.
Hesaplamalar, bu fonksiyonun -2, -1, 0, 1, 2 noktalarındaki değerlerinin yukarıdaki tabloda tam olarak tanımlandığını göstermektedir. Ancak bu fonksiyonun grafiği hiç de düz bir çizgi değildir (Şekil 49'da gösterilmektedir). Başka bir örnek fonksiyon olabilir y = x + l + sinπx; anlamları da yukarıdaki tabloda açıklanmıştır.

Bu örnekler, "saf" haliyle, birkaç noktayı kullanarak bir grafiği çizme yönteminin güvenilmez olduğunu göstermektedir. Bu nedenle, belirli bir fonksiyonun grafiğini çizmek için genellikle aşağıdaki şekilde hareket edilir. İlk olarak, grafiğin bir taslağını oluşturabileceğimiz bu fonksiyonun özelliklerini inceliyoruz. Daha sonra, fonksiyonun değerleri birkaç noktada hesaplanarak (seçimi fonksiyonun belirlenmiş özelliklerine bağlıdır), grafiğin karşılık gelen noktaları bulunur. Son olarak bu fonksiyonun özellikleri kullanılarak oluşturulan noktalar üzerinden bir eğri çizilir.
Daha sonra grafik çizimi bulmak için kullanılan fonksiyonların bazı (en basit ve en sık kullanılan) özelliklerine bakacağız, ancak şimdi grafik oluşturmak için yaygın olarak kullanılan bazı yöntemlere bakacağız.
y = |f(x)| fonksiyonunun grafiği.
Bir fonksiyonun grafiğini çizmek çoğu zaman gereklidir y = |f(x)|, nerede f(x) - verilen fonksiyon. Bunun nasıl yapıldığını size hatırlatalım. Bir sayının mutlak değerini tanımlayarak şunu yazabiliriz:
![]()
Bu, fonksiyonun grafiğinin şu anlama gelir: y =|f(x)| grafikten elde edilebilir, fonksiyon y = f(x)şu şekilde: fonksiyonun grafiğindeki tüm noktalar y = f(x) koordinatları negatif olmayanlar değiştirilmeden bırakılmalıdır; ayrıca, fonksiyonun grafiğindeki noktalar yerine y = f(x) Negatif koordinatlara sahipseniz, fonksiyonun grafiğinde karşılık gelen noktaları oluşturmalısınız. y = -f(x)(yani fonksiyonun grafiğinin bir kısmı
y = f(x) eksenin altında yer alan X, eksen etrafında simetrik olarak yansıtılmalıdır X).

Örnek 2. Fonksiyonun grafiğini çizin y = |x|.
Fonksiyonun grafiğini alalım y = x(Şekil 50, a) ve bu grafiğin bir kısmı X< 0 (eksenin altında yatan X) eksene göre simetrik olarak yansıtılır X. Sonuç olarak fonksiyonun grafiğini elde ederiz. y = |x|(Şekil 50, b).
Örnek 3. Fonksiyonun grafiğini çizin y = |x 2 - 2x|.

İlk önce fonksiyonun grafiğini çizelim y = x 2 - 2x. Bu fonksiyonun grafiği, dalları yukarı doğru yönlendirilmiş bir paraboldür, parabolün tepe noktası (1; -1) koordinatlarına sahiptir, grafiği x eksenini 0 ve 2 noktalarında keser. (0; 2) fonksiyon negatif değerler alır, dolayısıyla grafiğin bu kısmı apsis eksenine göre simetrik olarak yansıtılır. Şekil 51 fonksiyonun grafiğini göstermektedir y = |x 2 -2x|, fonksiyonun grafiğine dayanarak y = x 2 - 2x
y = f(x) + g(x) fonksiyonunun grafiği
Bir fonksiyonun grafiğini oluşturma problemini düşünün y = f(x) + g(x). fonksiyon grafikleri verilirse y = f(x) Ve y = g(x).
Fonksiyonun tanım tanım kümesinin y = |f(x) + g(x)| hem y = f(x) hem de y = g(x) fonksiyonlarının tanımlandığı tüm x değerlerinin kümesidir, yani bu tanım alanı, tanım alanlarının, f(x) fonksiyonlarının kesişimidir. ve g(x).
Bırakın puanlar (x 0, y 1) Ve (x 0, y 2) sırasıyla fonksiyonların grafiklerine aittir y = f(x) Ve y = g(x) yani y 1 = f(x 0), y 2 = g(x 0). O halde (x0;.y1 + y2) noktası fonksiyonun grafiğine aittir. y = f(x) + g(x)(için f(x 0) + g(x 0) = y 1 +y2),. ve fonksiyonun grafiğindeki herhangi bir nokta y = f(x) + g(x) bu şekilde elde edilebilir. Bu nedenle fonksiyonun grafiği y = f(x) + g(x) fonksiyon grafiklerinden elde edilebilir y = f(x). Ve y = g(x) her noktayı değiştirerek ( x n, y 1) fonksiyon grafikleri y = f(x) nokta (xn, y 1 + y 2), Nerede y 2 = g(xn), yani her noktayı kaydırarak ( x n, y 1) fonksiyon grafiği y = f(x) eksen boyunca en miktara göre y 1 = g(xn). Bu durumda sadece bu noktalar dikkate alınır X n her iki fonksiyonun da tanımlandığı y = f(x) Ve y = g(x).
Bir işlevi çizmenin bu yöntemi y = f(x) + g(x)) fonksiyonların grafiklerinin toplamı olarak adlandırılır y = f(x) Ve y = g(x)
Örnek 4. Şekilde fonksiyonun grafiği, grafik ekleme yöntemi kullanılarak oluşturulmuştur.
y = x + sinx.
Bir fonksiyonun grafiğini çizerken y = x + sinx bunu düşündük f(x) = x, A g(x) = sinx. Fonksiyon grafiğini çizmek için apsisleri -1,5π, -, -0,5, 0, 0,5,, 1,5, 2 olan noktaları seçiyoruz. f(x) = x, g(x) = sinx, y = x + sinx Seçilen noktalarda hesaplama yapıp sonuçları tabloya yerleştirelim.
Daha önce diğer fonksiyonları incelemiştik, örneğin doğrusal, standart formunu hatırlayalım:
dolayısıyla bariz temel fark - doğrusal fonksiyonda X birinci derecede yer alır ve çalışmaya başladığımız yeni fonksiyonda, X ikinci kuvvete karşılık gelir.
Doğrusal bir fonksiyonun grafiğinin düz bir çizgi olduğunu ve göreceğimiz gibi bir fonksiyonun grafiğinin parabol adı verilen bir eğri olduğunu hatırlayın.
Formülün nereden geldiğini öğrenerek başlayalım. Açıklaması şu: Eğer bize kenarı olan bir kare verilirse A, o zaman alanını şu şekilde hesaplayabiliriz:
Karenin bir kenar uzunluğunu değiştirirsek alanı da değişir.
Dolayısıyla fonksiyonun incelenmesinin nedenlerinden biri de budur.
Değişkeni hatırlayın X- bu bağımsız bir değişken veya argümandır; fiziksel bir yorumda örneğin zaman olabilir. Uzaklık ise tam tersine bağımlı bir değişkendir; zamana bağlıdır. Bağımlı değişken veya işlev bir değişkendir en.
Bu, her bir değerin geçerli olduğu yazışma yasasıdır. X tek bir değer atanır en.
Herhangi bir yazışma yasası, argümandan fonksiyona kadar benzersizlik gerekliliğini karşılamalıdır. Fiziksel bir yorumda, mesafenin zamana bağımlılığı örneğini kullanarak bu oldukça açık görünüyor: zamanın her anında başlangıç noktasından belirli bir mesafedeyiz ve başlangıçtan hem 10 hem de 20 kilometre uzakta olmamız imkansız. yolculuğun aynı zamanda t zamanında.
Aynı zamanda her fonksiyon değerine birden fazla argüman değeri ile ulaşılabilir.
Yani fonksiyonun grafiğini oluşturmamız gerekiyor, bunun için bir tablo yapmamız gerekiyor. Daha sonra grafiği kullanarak fonksiyonu ve özelliklerini inceleyin. Ancak fonksiyonun türüne dayalı bir grafik oluşturmadan önce bile, onun özellikleri hakkında bir şeyler söyleyebiliriz: açıktır ki en negatif değer alamaz çünkü
O halde bir tablo oluşturalım:

Pirinç. 1
Grafikten aşağıdaki özellikleri not etmek kolaydır:
Eksen en- bu grafiğin simetri eksenidir;
Parabolün tepe noktası (0; 0) noktasıdır;
Fonksiyonun sadece negatif olmayan değerleri kabul ettiğini görüyoruz;
Bulunduğu aralıkta ![]() fonksiyon azalır ve fonksiyonun arttığı aralıkta;
fonksiyon azalır ve fonksiyonun arttığı aralıkta;
Fonksiyon en küçük değerini tepe noktasında alır, ![]() ;
;
Bir fonksiyonun en büyük değeri yoktur;
örnek 1
Durum:
![]()
Çözüm:
Çünkü X Belirli bir aralıktaki koşul değişiklikleriyle, fonksiyon hakkında belirli bir aralıkta arttığını ve değiştiğini söyleyebiliriz. Fonksiyonun bu aralıkta bir minimum değeri ve bir maksimum değeri vardır.

Pirinç. 2. y = x 2 , x ∈ fonksiyonunun grafiği
Örnek 2
Durum: Bir fonksiyonun en büyük ve en küçük değerini bulun:
![]()
Çözüm:
X aralık boyunca değişir, yani en while aralığında azalır ve while aralığında artar.
Yani değişimin sınırları X ve değişimin sınırları en ve dolayısıyla belirli bir aralıkta fonksiyonun hem minimum değeri hem de maksimumu vardır.

Pirinç. 3. y = x 2 , x ∈ [-3; 2]
Aynı fonksiyon değerinin birden fazla argüman değeriyle elde edilebileceğini örnekleyelim.
Ders: Bir parabol veya ikinci dereceden fonksiyon nasıl oluşturulur?
TEORİK BÖLÜM
Parabol, ax 2 +bx+c=0 formülüyle tanımlanan bir fonksiyonun grafiğidir.
Bir parabol oluşturmak için basit bir algoritma izlemeniz gerekir:
1) Parabol formülü y=ax 2 +bx+c,
Eğer a>0 daha sonra parabolün dalları yönlendirilir yukarı,
aksi takdirde parabolün dalları yönlendirilir aşağı.
Ücretsiz Üye C bu nokta parabolün OY ekseniyle kesiştiği yerdir;
2), formül kullanılarak bulunur x=(-b)/2a bulunan x'i parabol denkleminde yerine koyarız ve buluruz sen;
3)Fonksiyon sıfırları veya başka bir deyişle parabolün OX ekseni ile kesişme noktalarına denklemin kökleri de denir. Kökleri bulmak için denklemi 0'a eşitleriz balta 2 +bx+c=0;
Denklem türleri:
a) Tam ikinci dereceden denklem şu şekildedir: balta 2 +bx+c=0 ve diskriminant tarafından çözülür;
b) Formun ikinci dereceden eksik denklemi balta 2 +bx=0. Bunu çözmek için, x'i parantezlerden çıkarmanız ve ardından her faktörü 0'a eşitlemeniz gerekir:
balta 2 +bx=0,
x(ax+b)=0,
x=0 ve ax+b=0;
c) Formun ikinci dereceden eksik denklemi balta 2 +c=0. Bunu çözmek için bilinmeyenleri bir tarafa, bilinenleri diğer tarafa taşımanız gerekir. x =±√(c/a);
4) Fonksiyonu oluşturmak için birkaç ek nokta bulun.
PRATİK BÖLÜM
Şimdi bir örnek kullanarak her şeyi adım adım analiz edeceğiz:
Örnek 1:
y=x 2 +4x+3
c=3, parabolün OY'yi x=0 y=3 noktasında kestiği anlamına gelir. a=1 1>0 olduğundan parabolün dalları yukarı bakar.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 köşe noktası (-2;-1) noktasındadır
x 2 +4x+3=0 denkleminin köklerini bulalım
Diskriminant kullanarak kökleri buluruz
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
x = -2 köşesinin yakınında bulunan birkaç rastgele noktayı alalım
x -4 -3 -1 0
y 3 0 0 3
y=x denkleminde x yerine 2 +4x+3 değerleri yazın
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Parabolün x = -2 düz çizgisine göre simetrik olduğu fonksiyon değerlerinden görülebilir.
Örnek #2:
y=-x 2 +4x
c=0, parabolün OY'yi x=0 y=0 noktasında kestiği anlamına gelir. a=-1 -1 olduğundan parabolün dalları aşağıya bakıyor -x 2 +4x=0 denkleminin köklerini bulalım
ax 2 +bx=0 formundaki tamamlanmamış ikinci dereceden denklem. Bunu çözmek için parantezlerden x'i çıkarmanız ve ardından her faktörü 0'a eşitlemeniz gerekir.
x(-x+4)=0, x=0 ve x=4.
x=2 tepe noktasına yakın konumdaki birkaç rastgele noktayı alalım.
x 0 1 3 4
y 0 3 3 0
y=-x denkleminde x yerine 2 +4x değerlerini yazın
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Parabolün x = 2 doğrusuna göre simetrik olduğu fonksiyon değerlerinden görülebilmektedir.
Örnek No.3
y=x 2 -4
c=4, parabolün OY'yi x=0 y=4 noktasında kestiği anlamına gelir. a=1 1>0 olduğundan parabolün dalları yukarı bakar.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 köşe noktası (0;-) noktasındadır 4)
x 2 -4=0 denkleminin köklerini bulalım
ax 2 +c=0 formundaki tamamlanmamış ikinci dereceden denklem. Bunu çözmek için bilinmeyenleri bir tarafa, bilinenleri diğer tarafa taşımanız gerekir. x =±√(c/a)
x 2 =4
x 1 =2
x2 =-2
x=0 tepe noktasına yakın konumdaki birkaç rastgele noktayı alalım
x -2 -1 1 2
y 0 -3 -3 0
y= x 2 -4 değerleri denkleminde x yerine yerine koyun
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Parabolün x = 0 düz çizgisine göre simetrik olduğu fonksiyon değerlerinden görülebilir.
Abone YOUTUBE'daki kanala tüm yeni ürünlerden haberdar olmak ve sınavlara bizimle hazırlanmak için.
“Doğal logaritma” - 0.1. Doğal logaritmalar. 4. Logaritmik dart. 0.04. 7.121.
“Güç fonksiyonu derecesi 9” - U. Kübik parabol. Y = x3. 9. sınıf öğretmeni Ladoshkina I.A. Y = x2. Hiperbol. 0. Y = xn, y = x-n burada n belirli bir doğal sayıdır. X. Üs çift bir doğal sayıdır (2n).
“İkinci dereceden fonksiyon” - 1 İkinci dereceden fonksiyonun tanımı 2 Bir fonksiyonun özellikleri 3 Bir fonksiyonun grafikleri 4 İkinci dereceden eşitsizlikler 5 Sonuç. Özellikler: Eşitsizlikler: 8A sınıfı öğrencisi Andrey Gerlitz tarafından hazırlanmıştır. Plan: Grafik: -a için monotonluk aralıkları > a için 0< 0. Квадратичная функция. Квадратичные функции используются уже много лет.
“İkinci dereceden fonksiyon ve grafiği” - Çözüm.y=4x A(0.5:1) 1=1 A- aittir. a=1 olduğunda y=ax formülü alınır.
“8. sınıf ikinci dereceden fonksiyon” - 1) Bir parabolün tepe noktasını oluşturun. İkinci dereceden bir fonksiyonun grafiğinin çizilmesi. X. -7. Fonksiyonun grafiğini oluşturun. Cebir 8. sınıf Öğretmeni 496 Bovina okulu T.V.-1. Inşaat planı. 2) x=-1 simetri eksenini oluşturun. y.