Funkcja budowania
Oferujemy Państwu usługę konstruowania wykresów funkcji online, do której wszelkie prawa należą do firmy Desmos. Użyj lewej kolumny, aby wprowadzić funkcje. Można wprowadzić ręcznie lub korzystając z wirtualnej klawiatury znajdującej się na dole okna. Aby powiększyć okno z wykresem, możesz ukryć zarówno lewą kolumnę, jak i wirtualną klawiaturę.
Korzyści z wykresów online
- Wizualna prezentacja wprowadzonych funkcji
- Tworzenie bardzo złożonych wykresów
- Konstrukcja wykresów określonych pośrednio (na przykład elipsa x^2/9+y^2/16=1)
- Możliwość zapisywania wykresów i otrzymywania linku do nich, który staje się dostępny dla każdego w Internecie
- Kontrola skali, koloru linii
- Możliwość kreślenia wykresów punktowo, z wykorzystaniem stałych
- Jednoczesne rysowanie kilku wykresów funkcji
- Wykreślanie współrzędnych biegunowych (użyj r i θ(\theta))
Z nami łatwo jest budować wykresy o różnej złożoności online. Budowa odbywa się błyskawicznie. Usługa jest potrzebna do znajdowania punktów przecięcia funkcji, do przedstawiania wykresów w celu dalszego przenoszenia ich do dokumentu Word jako ilustracji przy rozwiązywaniu problemów oraz do analizowania cech behawioralnych wykresów funkcji. Optymalną przeglądarką do pracy z wykresami na tej stronie serwisu jest Google Chrome. Nie gwarantuje się poprawnego działania w przypadku korzystania z innych przeglądarek.
Wybierzmy na płaszczyźnie prostokątny układ współrzędnych i narysujmy wartości argumentu na osi odciętych X, a na rzędnej - wartości funkcji y = f(x).
Wykres funkcji y = f(x) to zbiór wszystkich punktów, których odcięte należą do dziedziny definicji funkcji, a rzędne są równe odpowiednim wartościom funkcji.
Innymi słowy wykres funkcji y = f (x) jest zbiorem wszystkich punktów płaszczyzny, współrzędnych X, Na które spełniają relację y = f(x).

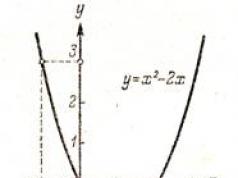
Na ryc. Rys. 45 i 46 przedstawiają wykresy funkcji y = 2x + 1 I y = x 2 - 2x.
Ściśle rzecz biorąc, należy rozróżnić wykres funkcji (której dokładną matematyczną definicję podano powyżej) od narysowanej krzywej, która zawsze daje jedynie mniej lub bardziej dokładny szkic wykresu (a nawet wtedy z reguły nie cały wykres, a jedynie jego część zlokalizowana w końcowych częściach płaszczyzny). Jednakże w dalszej części będziemy zazwyczaj mówić „wykres”, a nie „szkic wykresu”.
Korzystając z wykresu, możesz znaleźć wartość funkcji w punkcie. Mianowicie, jeśli o to chodzi x = a należy do dziedziny definicji funkcji y = f(x), a następnie znajdź numer fa)(tj. wartości funkcji w punkcie x = a) powinieneś to zrobić. Jest to konieczne przez punkt odciętej x = a narysuj linię prostą równoległą do osi rzędnych; ta prosta przetnie wykres funkcji y = f(x) w jednym punkcie; rzędna tego punktu będzie, zgodnie z definicją wykresu, równa fa)(ryc. 47).

Na przykład dla funkcji f(x) = x 2 - 2x korzystając z wykresu (ryc. 46) znajdujemy f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 itd.
Wykres funkcji wyraźnie ilustruje zachowanie i właściwości funkcji. Na przykład, biorąc pod uwagę rys. 46 jasne jest, że funkcja y = x 2 - 2x przyjmuje wartości dodatnie, gdy X< 0 i o godz x > 2, ujemny - przy 0< x < 2; наименьшее значение функция y = x 2 - 2x przyjmuje o godz x = 1.
Aby wykreślić funkcję k(x) musisz znaleźć wszystkie punkty płaszczyzny, współrzędne X,Na które spełniają równanie y = f(x). W większości przypadków nie da się tego zrobić, ponieważ istnieje nieskończona liczba takich punktów. Dlatego wykres funkcji jest przedstawiony w przybliżeniu - z większą lub mniejszą dokładnością. Najprostsza jest metoda wykreślenia wykresu z wykorzystaniem kilku punktów. Polega ona na tym, że argument X podaj skończoną liczbę wartości - powiedzmy x 1, x 2, x 3,..., x k i utwórz tabelę zawierającą wartości wybranych funkcji.
Tabela wygląda następująco:
Po skompilowaniu takiej tabeli możemy zarysować kilka punktów na wykresie funkcji y = f(x). Następnie łącząc te punkty gładką linią otrzymujemy przybliżony widok wykresu funkcji y = f(x).
Należy jednak zaznaczyć, że metoda wykresu wielopunktowego jest bardzo zawodna. W rzeczywistości zachowanie wykresu pomiędzy zamierzonymi punktami i jego zachowanie poza odcinkiem pomiędzy wziętymi skrajnymi punktami pozostaje nieznane.
Przykład 1. Aby wykreślić funkcję y = f(x) ktoś skompilował tabelę wartości argumentów i funkcji:
Odpowiednie pięć punktów pokazano na ryc. 48.

Na podstawie położenia tych punktów doszedł do wniosku, że wykres funkcji jest linią prostą (pokazaną na rys. 48 linią przerywaną). Czy wniosek ten można uznać za wiarygodny? O ile nie istnieją dodatkowe względy na poparcie tego wniosku, trudno go uznać za wiarygodny. niezawodny.
Aby uzasadnić nasze stwierdzenie, rozważmy funkcję
![]() .
.
Z obliczeń wynika, że wartości tej funkcji w punktach -2, -1, 0, 1, 2 dokładnie opisuje powyższa tabela. Wykres tej funkcji wcale nie jest jednak linią prostą (pokazuje to rys. 49). Innym przykładem może być funkcja y = x + l + sinπx; jego znaczenie opisano również w tabeli powyżej.

Przykłady te pokazują, że w „czystej” postaci metoda wykreślania wykresu z wykorzystaniem kilku punktów jest zawodna. Dlatego też, aby wykreślić wykres danej funkcji, zwykle postępuje się w następujący sposób. Najpierw badamy właściwości tej funkcji, za pomocą których możemy zbudować szkic wykresu. Następnie, obliczając wartości funkcji w kilku punktach (których wybór zależy od ustalonych właściwości funkcji), znajdują się odpowiednie punkty wykresu. Na koniec przez skonstruowane punkty rysuje się krzywą, wykorzystując właściwości tej funkcji.
Niektórym (najprostszym i najczęściej używanym) właściwościom funkcji używanych do wyszukiwania szkicu grafu przyjrzymy się później, ale teraz przyjrzymy się niektórym powszechnie stosowanym metodom konstruowania grafów.
Wykres funkcji y = |f(x)|.
Często konieczne jest wykreślenie funkcji y = |f(x)|, gdzie f(x) - dana funkcja. Przypomnijmy, jak to się robi. Definiując wartość bezwzględną liczby, możemy pisać
![]()
Oznacza to, że wykres funkcji y =|f(x)| można uzyskać z wykresu funkcji y = f(x) w następujący sposób: wszystkie punkty na wykresie funkcji y = f(x), którego rzędne są nieujemne, należy pozostawić bez zmian; dalej zamiast punktów wykresu funkcji y = f(x) mając współrzędne ujemne, należy skonstruować odpowiednie punkty na wykresie funkcji y = -f(x)(tj. część wykresu funkcji
y = f(x), która leży poniżej osi X, powinny być odzwierciedlone symetrycznie względem osi X).

Przykład 2. Wykres funkcji y = |x|.
Weźmy wykres funkcji y = x(ryc. 50, a) i część tego wykresu o godz X< 0 (leży pod osią X) symetrycznie odbite względem osi X. W rezultacie otrzymujemy wykres funkcji y = |x|(ryc. 50, b).
Przykład 3. Wykres funkcji y = |x 2 - 2x|.

Najpierw narysujmy funkcję y = x 2 - 2x. Wykres tej funkcji jest parabolą, której gałęzie są skierowane w górę, wierzchołek paraboli ma współrzędne (1; -1), jej wykres przecina oś x w punktach 0 i 2. W przedziale (0; 2) funkcja przyjmuje wartości ujemne, dlatego ta część wykresu jest odzwierciedlona symetrycznie względem osi odciętych. Rysunek 51 przedstawia wykres funkcji y = |x 2 -2x|, na podstawie wykresu funkcji y = x 2 - 2x
Wykres funkcji y = f(x) + g(x)
Rozważmy problem skonstruowania wykresu funkcji y = f(x) + g(x). jeśli podane są wykresy funkcji y = f(x) I y = g(x).
Należy zauważyć, że dziedzina definicji funkcji y = |f(x) + g(x)| to zbiór wszystkich wartości x, dla których zdefiniowane są obie funkcje y = f(x) i y = g(x), tj. ta dziedzina definicji jest przecięciem dziedzin definicji, funkcji f(x) i g(x).
Niech punkty (x 0 , y 1) I (x 0, y 2) należą odpowiednio do wykresów funkcji y = f(x) I y = g(x), tj. y 1 = f(x 0), y 2 = g(x 0). Wtedy punkt (x0;. y1 + y2) należy do wykresu funkcji y = f(x) + g(x)(Do f(x 0) + g(x 0) = y 1 +y2),. i dowolny punkt na wykresie funkcji y = f(x) + g(x) można uzyskać w ten sposób. Dlatego wykres funkcji y = f(x) + g(x) można uzyskać z wykresów funkcji y = f(x). I y = g(x) zastępując każdy punkt ( x n, y 1) grafika funkcyjna y = f(x) kropka (x n, y 1 + y 2), Gdzie y 2 = g(x n), czyli przesuwając każdy punkt ( x n, y 1) wykres funkcji y = f(x) wzdłuż osi Na według kwoty y 1 = g(x n). W tym przypadku brane są pod uwagę tylko takie punkty X n, dla którego zdefiniowano obie funkcje y = f(x) I y = g(x).
Ta metoda wykreślania funkcji y = f(x) + g(x) nazywa się dodawaniem wykresów funkcji y = f(x) I y = g(x)
Przykład 4. Na rysunku skonstruowano wykres funkcji metodą dodawania wykresów
y = x + sinx.
Podczas kreślenia funkcji y = x + sinx tak myśleliśmy f(x) = x, A g(x) = sinx. Aby wykreślić wykres funkcji, wybieramy punkty z odciętymi -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Wartości f(x) = x, g(x) = sinx, y = x + sinx Wykonajmy obliczenia w wybranych punktach i umieśćmy wyniki w tabeli.
Wcześniej badaliśmy inne funkcje, na przykład liniową, przypomnijmy jej standardową postać:
stąd oczywista zasadnicza różnica - w funkcji liniowej X stoi w pierwszym stopniu i w nowej funkcji zaczynamy się uczyć, X stoi do drugiej potęgi.
Przypomnijmy, że wykres funkcji liniowej jest linią prostą, a wykres funkcji, jak zobaczymy, jest krzywą zwaną parabolą.
Zacznijmy od ustalenia, skąd wzięła się formuła. Wyjaśnienie jest następujące: jeśli dany jest kwadrat z bokiem A, to możemy obliczyć jego pole w następujący sposób:
Jeśli zmienimy długość boku kwadratu, to zmieni się jego pole.
Jest to więc jeden z powodów, dla których bada się tę funkcję
Przypomnijmy, że zmienna X- jest to zmienna niezależna, czyli argument, w interpretacji fizycznej może to być np. czas. Odległość jest natomiast zmienną zależną, zależy od czasu. Zmienna zależna lub funkcja jest zmienną Na.
Jest to prawo korespondencji, zgodnie z którym każda wartość X przypisana jest pojedyncza wartość Na.
Każde prawo korespondencyjne musi spełniać wymóg wyjątkowości od argumentu do funkcji. W interpretacji fizycznej wygląda to całkiem jasno na przykładzie zależności odległości od czasu: w każdym momencie jesteśmy w pewnej odległości od punktu początkowego, a nie da się być jednocześnie 10 i 20 kilometrów od początku podróży w tym samym czasie w chwili t.
Jednocześnie każdą wartość funkcji można osiągnąć za pomocą kilku wartości argumentów.
Musimy więc zbudować wykres funkcji, w tym celu musimy stworzyć tabelę. Następnie przeanalizuj funkcję i jej właściwości za pomocą wykresu. Ale jeszcze zanim zbudujemy wykres na podstawie rodzaju funkcji, możemy powiedzieć coś o jej właściwościach: to oczywiste Na nie może przyjmować wartości ujemnych, ponieważ
Zróbmy więc tabelę:

Ryż. 1
Z wykresu łatwo zauważyć następujące właściwości:
Oś Na- jest to oś symetrii wykresu;
Wierzchołek paraboli to punkt (0; 0);
Widzimy, że funkcja przyjmuje tylko wartości nieujemne;
W przedziale gdzie ![]() funkcja maleje i na przedziale, w którym funkcja rośnie;
funkcja maleje i na przedziale, w którym funkcja rośnie;
Funkcja uzyskuje najmniejszą wartość w wierzchołku, ![]() ;
;
Nie ma największej wartości funkcji;
Przykład 1
Stan : schorzenie:
![]()
Rozwiązanie:
Ponieważ X poprzez zmianę warunku w określonym przedziale, możemy powiedzieć o funkcji, że rośnie i zmienia się w tym przedziale. Funkcja ma w tym przedziale wartość minimalną i maksymalną

Ryż. 2. Wykres funkcji y = x 2 , x ∈
Przykład 2
Stan : schorzenie: Znajdź największą i najmniejszą wartość funkcji:
![]()
Rozwiązanie:
X zmienia się w danym przedziale, co oznacza Na maleje w przedziale while i wzrasta w przedziale while .
A więc granice zmian X i granice zmian Na, a zatem w danym przedziale istnieje zarówno minimalna wartość funkcji, jak i maksimum

Ryż. 3. Wykres funkcji y = x 2 , x ∈ [-3; 2]
Zilustrujmy fakt, że tę samą wartość funkcji można osiągnąć za pomocą kilku wartości argumentów.
Lekcja: Jak skonstruować parabolę lub funkcję kwadratową?
CZĘŚĆ TEORETYCZNA
Parabola jest wykresem funkcji opisanej wzorem ax 2 +bx+c=0.
Aby zbudować parabolę, należy postępować zgodnie z prostym algorytmem:
1) Wzór na parabolę y=ax 2 +bx+c,
Jeśli a>0 wówczas skierowane są gałęzie paraboli w górę,
w przeciwnym razie gałęzie paraboli są skierowane w dół.
Wolny Członek C punkt ten przecina parabolę z osią OY;
2), oblicza się za pomocą wzoru x=(-b)/2a, podstawiamy znaleziony x do równania paraboli i znajdujemy y;
3)Zera funkcji lub innymi słowy punkty przecięcia paraboli z osią OX, nazywane są również pierwiastkami równania. Aby znaleźć pierwiastki, przyrównujemy równanie do 0 topór 2 +bx+c=0;
Rodzaje równań:
a) Pełne równanie kwadratowe ma postać topór 2 +bx+c=0 i jest rozwiązywany przez dyskryminator;
b) Niepełne równanie kwadratowe postaci topór 2 +bx=0. Aby rozwiązać ten problem, musisz wyjąć x z nawiasów, a następnie przyrównać każdy współczynnik do 0:
topór 2 +bx=0,
x(ax+b)=0,
x=0 i ax+b=0;
c) Niepełne równanie kwadratowe postaci topór 2 +c=0. Aby go rozwiązać, musisz przesunąć niewiadome na jedną stronę, a wiadome na drugą. x =±√(c/a);
4) Znajdź kilka dodatkowych punktów, aby skonstruować funkcję.
CZĘŚĆ PRAKTYCZNA
I tak teraz na przykładzie przeanalizujemy wszystko krok po kroku:
Przykład 1:
y=x2 +4x+3
c=3 oznacza, że parabola przecina OY w punkcie x=0 y=3. Gałęzie paraboli patrzą w górę, ponieważ a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 wierzchołek znajduje się w punkcie (-2;-1)
Znajdźmy pierwiastki równania x 2 +4x+3=0
Używając dyskryminatora, znajdujemy pierwiastki
a=1 b=4 c=3
D=b2-4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Weźmy kilka dowolnych punktów znajdujących się w pobliżu wierzchołka x = -2
x -4 -3 -1 0
y 3 0 0 3
Zamiast x wstaw do równania y=x 2 +4x+3 wartości
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Z wartości funkcji widać, że parabola jest symetryczna względem prostej x = -2
Przykład nr 2:
y=-x 2 +4x
c=0 oznacza, że parabola przecina OY w punkcie x=0 y=0. Gałęzie paraboli skierowane są w dół, ponieważ a=-1 -1 Znajdźmy pierwiastki równania -x 2 +4x=0
Niepełne równanie kwadratowe postaci ax 2 +bx=0. Aby rozwiązać ten problem, należy wyjąć x z nawiasów i przyrównać każdy współczynnik do 0.
x(-x+4)=0, x=0 i x=4.
Weźmy kilka dowolnych punktów znajdujących się w pobliżu wierzchołka x=2
x 0 1 3 4
y 0 3 3 0
Zamiast x wstaw do równania y=-x 2 +4x wartości
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Z wartości funkcji widać, że parabola jest symetryczna względem prostej x = 2
Przykład nr 3
y=x 2 -4
c=4 oznacza, że parabola przecina OY w punkcie x=0 y=4. Gałęzie paraboli są skierowane w górę, ponieważ a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 wierzchołek znajduje się w punkcie (0;- 4)
Znajdźmy pierwiastki równania x 2 -4=0
Niepełne równanie kwadratowe postaci ax 2 +c=0. Aby go rozwiązać, musisz przesunąć niewiadome na jedną stronę, a wiadome na drugą. x =±√(c/a)
x2 =4
x 1 = 2
x2 =-2
Weźmy kilka dowolnych punktów znajdujących się w pobliżu wierzchołka x=0
x -2 -1 1 2
y 0 -3 -3 0
Zamiast x wstaw do równania y= x 2 -4 wartości
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Z wartości funkcji widać, że parabola jest symetryczna względem prostej x = 0
Subskrybuj na kanał na YOUTUBE aby być na bieżąco ze wszystkimi nowościami produktowymi i przygotowywać się z nami do egzaminów.
„Logarytm naturalny” - 0,1. Logarytmy naturalne. 4. Rzutki logarytmiczne. 0,04. 7.121.
„Funkcja mocy stopień 9” - U. Parabola sześcienna. Y = x3. Nauczycielka 9. klasy Ladoshkina I.A. Y = x2. Hiperbola. 0. Y = xn, y = x-n gdzie n jest daną liczbą naturalną. X. Wykładnik jest parzystą liczbą naturalną (2n).
„Funkcja kwadratowa” - 1 Definicja funkcji kwadratowej 2 Własności funkcji 3 Wykresy funkcji 4 Nierówności kwadratowe 5 Wniosek. Właściwości: Nierówności: Opracowano przez ucznia klasy 8A Andreya Gerlitza. Plan: Wykres: -Przedziały monotoniczności dla a > 0 dla a< 0. Квадратичная функция. Квадратичные функции используются уже много лет.
„Funkcja kwadratowa i jej wykres” - Rozwiązanie.y=4x A(0,5:1) 1=1 A-należy. Gdy a=1, wzór y=ax przyjmuje postać.
„Funkcja kwadratowa ósmej klasy” - 1) Skonstruuj wierzchołek paraboli. Rysowanie wykresu funkcji kwadratowej. X. -7. Zbuduj wykres funkcji. Algebra 8. klasy Nauczyciel 496 Bovina school T.V. -1. Plan budowy. 2) Skonstruuj oś symetrii x=-1. y.